Pieces of Information – Color-Changing Cephalopods, a Machine That Turns Itself Off and Other Stories

Dumbo octopus. NOAA Okeanos Explorer Program, Oceano Profundo 2015; Exploring Puerto Rico’s Seamounts, Trenches, and Troughs.

[This text was first published in Occulto h: Limits , released in November 2017]

Hey Hey Hey

Industry creation a creation in the equation why why etc. Why equally 8X eight eight a ex and X Plus babe why am ex are the variables–Space–White why while ANB are the constants that had passed that headache asked that hand hey hey hey asked as us define devalue the value call of the variables. Constance cons done Constance and marvelous and Mario Brothers Barrientos Mario Brothers hey I need each other baggy bodily badly not only in the world of numbers.

The quote above is the beginning of the editorial text I wrote for Occulto π (2014), in a new version performed by me and transcribed by the native dictation function of my computer. The original reads,

In the equation y = ax + b, y and x are the variables – the value of the former depending upon the value of the latter – while a and b are the constants that help us define the value of the variables. Constants and variables need each other badly not only in the world of numbers.

Something clearly went wrong during the transmission of the vocal message and its conversion into written text. I will be fair and admit it wasn’t just the machine’s fault: my natural Italian cadence, contaminated by seven years in Germany, is no example of a perfect English accent, and I repeated some words several times out of frustration. It was only a first attempt, and the dictation tool is supposed to get used to the way you speak and improve with time, as the last eight correct words “badly not only in the world of numbers” seem to confirm. On the bright side, the poor transcription has that certain Dadaesque, nonsense charm that the original version completely lacked.
The story of this little experiment reveals many things about how communication works: the decisions (and mistakes) that can be made while formulating an arbitrary message, what can go wrong while sending it depending on the media you use and the general conditions, the difficulties the receiver/recipient can encounter during the interpretation and reproduction, the tension between intentional and unintentional elements … It sounds like a complex, hard to control affair. Or is it?

Communication theory, also known as information theory, can be defined in short and simple words as the mathematical description of a generalized communication system. It’s also one of those fortunate cases in science history where we know exactly when a theory was born, who thought about it first, and we even have a publication with which the theory properly started, namely “A Mathematical Theory of Communication”, by Claude E. Shannon – mathematician and engineer – first published in the Bell System Technical Journal in July 1948. With this paper and the work behind it, Shannon went to the very core of communication systems from a quantitative point of view, and unified them under a minimal yet precise and reliable structure. In doing this, he paved the way to a complete new field and to many, many applications – data storage and data compression are but two major examples, and if we were to mention all the technologies in which the theory is heavily involved, we would have to list modern computers, the internet, smart phones and pretty much whatever the telecommunication industry is currently producing; all things that play a huge role in our lives and society. In a way, the importance and impact of its applications may have stolen the spotlight from the intellectual value and cultural relevance at large of the theory¹.

The present essay will therefore try not to be another ‘Father of the Information Age’ story, and rather highlight Shannon’s ability to ‘extract’ a purely mathematical structure and quantitative universal parameters from what many considered a scattered series of practical engineering issues, such as improving the efficiency of the electrical telegraph. The theory can be and has been applied back effectively to old and new technologies, but this didn’t really seem to be Shannon’s main preoccupation while writing “A Mathematical Theory of Communication” – an abstract, dense and highly technical forty-five-page paper, likely to scare away the readers who lack a more than decent mathematical education and/or a strong motivation. I dare make a parallel here between communication theory and two other major scientific results of the twentieth century, namely quantum theory and Einstein’s general relativity; all to be counted among the biggest intellectual achievements of humankind, each acting on very different scales. Quantum theory and relativity have effects that are mostly detectable on scales very far away from our daily life – either very small or very big – while communication theory is something happening in our everyday activity, over and over again, no matter who we are, where we are, or what kind of technology we have at disposal. It happens when we talk with somebody on the phone or in person, when we send or receive an email, when we sing or play for an audience, when we visit an art exhibition, when we watch a movie or listen to the radio, when we look at a kid’s drawing. Communication theory enabled modern computers, but communication doesn’t require one in order to be seen at work; in fact, it doesn’t even require the involvement of human beings, if we consider the sophisticated dances of the honey bee or the flamboyant color changes of cephalopods². Communication is a basic and universal process that offers a lot of accessible working material, to laymen as well; it is something we can try, and we do try, at home, all the time.

Close-up of octopus at approximately 2500 meters water depth. NOAA Okeanos Explorer Program, Galapagos Rift Expedition 2011.

The scheme laid out by Shannon looks straightforward. Communication through a (more or less reliable) channel – human speech through air, live music through amplifiers, projection of images through a beamer – involves a few recurring elements: information source, sent message, transmitter, signal, received signal, receiver, received message, destination and – last but not least, and unavoidable in real life – the noise source, something that Shannon defined, quantified and analyzed much better than anybody before. Noise here is not necessarily an unpleasant sound as in its most common meaning – it includes anything that disturbs the transmission of the message, it consists of a certain amount of extra, unintentional information that messes up the intentional one.

The little dictation story we started with involved the English language, both in his spoken and written version. Natural languages are, in fact, a sort of running gag in communication theory, they appear repeatedly in it, in many ways and many guises: as a model, a tool, an object to investigate, a limit to approach, a starting point, a goal, the simplest possible case or an example of complexity.
We will then temporarily leave aside the 1948 landmark paper, and look into another work by Shannon, published a couple of years later and focused on language.

“Prediction and Entropy of Printed English”

Claude E. Shannon’s “Prediction and Entropy of Printed English” was written in 1950 and published in 1951, again in the Bell System Technical Journal. The central issue of the paper is how precisely one can predict the next letter of an English text when n preceding letters are known. In other words, Shannon aims at developing a procedure to calculate the entropy and redundancy of the English language, having already defined what both terms mean in this context in his previous, most famous and already mentioned paper “A Mathematical Theory of Communication”.

Entropy – a term borrowed from physics – is a measure of the amount of information; in this case, it tells how much information is provided on average by a letter. You’ll probably agree with me if I say that, in general, information is provided when something new or unexpected comes up, based on several factors such as context, expectations and pre-existing knowledge. The very same thing – say the address of a shop selling cheap booze on a late Sunday night – is utterly trivial in a city like Berlin as much as rare or illegal in other parts of the world. Information has a lot to do with probability, it is a statistical parameter. In an alphabet where each letter has the same probability – i.e. each of them is equally (un)expected – the entropy value is very high and prediction methods are doomed to be much less effective. Yet the letters of natural languages do have different probability, for example the letter e is the most common in English and many other natural languages. And it’s not just about letters’ frequency: syntax and grammar must also be considered. Redundancy is the quantification of the limitations introduced by all these statistical properties, constraints, rules and guidelines.

e is the most frequent letter in English and several pother languages. Image Courtesy Stefan Juster.

The adjective ‘redundant’ has a negative connotation in its common use as well as in specific contexts such as computer programming or literary critic. Our first-grade school teacher wanted us to avoid repetitions in texts, and you may think that telling something that almost everybody knows or can easily guess is boring, so the more information, the better. Yet redundancy plays an important, positive role; in fact, it enables communication.

I lettori italiani (ciao!) capiranno queste parole, ma gli altri si staranno chiedendo se sono impazzita, o se è stato fatto un errore grossolano durante la correzione bozze.

If you read or listen to a language you don’t know, then you’re provided too much – too new, too unexpected! – information, and the message won’t reach you. Choosing a language, or, more in general, an encoding system that works well for your ‘audience’ – be it a bunch of humans or a machine – is of course essential. Even a conversation in your mother tongue can present some difficulties, for example if there are cars passing by or loud music in the background, but you can usually fill in the gaps when needed, just like you do during disturbed phone calls, or while reading badly scanned pages of a book with one or two missing characters at the beginning of each line. In short: Redundancy is what we already know, what we expect; entropy (information) is the unknown, the surprise. The cars passing by represent noise.

Any message can be ideally described as a selection of symbols (units) out of a set of possible symbols possessing statistical properties. (This holds also when we’re not talking about natural languages anymore.) The message usually presents a tension between ‘surprising’ elements that provide information, and predictable, redundant elements that help deliver and decipher it. A language whose alphabet and rules change continuously while speaking will be perceived as meaningless, while a completely predictable or already known pattern of words (or sounds, or images) will be discarded as trivial. Effective communication stays somewhere in between. Humanity brings such tension to its limits in certain cases – for example by using nonsense in literature or randomly generated sounds in music, or by creating codes for secret or internal communication – yet the intentional breaking of the rules somewhat confirms their value and relevance.

Communication of any kind always consists of a tension between freedom and constraints, randomness and order. Shannon is not an artist, he’s a mathematician, so he wants to measure these things, and the unit of measure he chooses is the binary digit, the bit. The entropy of the English language can then be expressed as the number of binary digits (bits) you need on average to encode efficiently a letter or a sequence of letters. The coding system should take into account the statistical properties of the language in order to become more efficient – a basic example of this can be found in the Morse code, in which the most common letter e corresponds to a single dot, the shortest possible symbol. The underlying principle is that doing better and faster the things you do very often will save time on the long run, even if you will occasionally waste some extra time on less usual ones – say if you have to transmit an experimental ten-page poem based on the letters q and z. Redundancy clearly plays an important role in such a process: redundant content or tasks can be somehow ‘grouped’, or compressed, without losing information. The blank space, for example, is almost completely redundant in natural languages: if we were to play a version of the hangman game based on sentences rather than single words, it would make sense to always choose the space as first guess. While working with an alphabet of 27 symbols that includes it, we could consider the space a sort of ‘default’ character and take advantage of that to optimize the encoding process. The first, ‘empty’ book of Kurd Laßwitz’s “Universalbibliothek” consisting of 1,000,000 blank spaces – more about that later – could be possibly compressed to 1 bit only, without any loss of information!

The first method to calculate the entropy of the English language illustrated by Claude Shannon in the ‘Prediction’ paper is based on existing statistical data and consists of a series of approximations F₀, F₁, F₂, … F_N – where N indicates an amount of characters corresponding to single letters, bigrams, trigrams … N-grams – that approach the entropy H as a limit. F₀ is a sort of trivial case, like guessing a random letter of the alphabet out of any context, F₁ deals with single letters taking into account their frequency, F₂ can rely on several statistical properties: the high frequency of certain bigrams in the English language, such as TH, the high probability of others when the first letter is known, as in QU, or the ‘impossibility’ – to a fair approximation – of others, such as WZ or QK (oops, I have just made them possible by typing them in an English printed text!). Things get harder with trigrams already: the groups of three letters bridging two words behave much differently than the ones inside words. In general: the longer the N-gram, the less reliable and precise the results, yet some interesting considerations can be made about the entropy of single vocables (F_word).

Series of approximations to English, from Shannon, “A Mathematical Theory of Communication”, 1948.

The most frequent word in English is ‘the’, followed by ‘of’, and so on. The maximum probability of anything is always 1, corresponding to 100%. Something with probability 1 will happen for sure, and its entropy will be equal to zero because, well, you already know it’s going to happen – no surprise. Let’s keep this in mind and consider the statistical frequency of words: their list could, in principle, go on forever, but it can’t in a formal context, because the total probability can’t be greater than 1, so a certain word (in Shannon’s table the one ranked 8,727th) will mark the critical point, and all words ranked lower will be assigned probability zero – yet, they exist, and we can use them! This paradox has an easy explanation in real life: most of the spoken and written communication going on in mainstream media, everyday conversations etc. uses a few thousand words; the rest of the vocabulary belongs to niche contexts such as academic discourse, technical documentation and subcultural movements, and can be considered ‘non-existent’ (statistically irrelevant) by convention, at least while looking at the big picture. This may not sound flattering if you’re struggling to finish a PhD on a minor historical issue in early modern science, or neglecting your money job to curate the program of an underground artist-run space; on the other hand, knowing your limits may help you downplay and relax a bit – don’t worry, nobody cares! – or unexpectedly encourage you to take up the challenge and widen your goals and horizons.

Another method used by Shannon consists of experiments with human participants that could be described as variations on the classic hangman game; they are all based on the fact that people have an incredibly rich, although mostly implicit statistical knowledge of the languages they can speak and write, especially of their mother tongue. In experiment 1, participants are asked to guess the letters of an English passage they’re not familiar with, one letter at a time, starting from the first one on the left. If a guess is right the participants can proceed with the next one, if the guess is wrong they are told the correct one. The results are written down this way: a first line with the complete original text, a second line with a dash line for each correct guess and the correct letter for each wrong guess, like that:

READING LAMP ON THE DESK SHED GLOW ON
REA———-O——D—-SHED-GLO–O-

The second line is nothing but a reduced version of the original text – reduced is the very word used by Shannon, but we may as well say ‘compressed’, and the term used in the German translation of the paper is, in fact, ‘komprimiert’. This reduced version contains the same information as the original text and one could at least in principle reconstruct the latter from it, assuming one could find an ideal Doppelgänger of the participant that would think in the same way and make exactly the same decisions.
Each single prediction – no matter if based on statistical tables or on human implicit knowledge – can be reduced to simple yes/no questions, which fits well also with the binary digit as unit of measure – 1/0, yes/no, open/closed, on/off. This can help us understand better what we mean by efficient coding. Say we are playing Guess Who, that is, you must guess a person I thought about by asking me a maximum of twenty questions. We start and the first steps go like this,

“Is this person Blixa Bargeld?”, you ask.
“No,” I answer.
“Is this person my mother?”
“No.”
“Is this person … Donald Trump?”
“Nope.”

As you see, you’re not doing well. There are so many possibilities, so many symbols in your ‘alphabet’ of all the people in the world, and you’re excluding only one with each question. You should better figure out smarter questions that will lead you to the solution faster.

“Is this person famous?”
“No.”
Voilà, you just excluded all the famous people in the world.
“Do I know this person?”
“Yes.”
Big step forward!
“Does this person live in the same city as me?”
And so on.

Back to the Point

We’ve just talked a lot about natural languages, but let’s not forget that the theory was born out of practical engineering problems. Here’s a list of the major communication systems that existed in 1948:

Telegraph (Morse, 1830s)
Telephone (Bell, 1876)
Wireless Telegraph (Marconi, 1887)
AM Radio (early 1900s)
Single-Sideband Modulation (Carson, 1922)
Television (1925–27)
Teletype (1931)
Frequency Modulation (Armstrong, 1936)
Pulse-Code Modulation (PCM) (Reeves, 1937–39)
Vocoder (Dudley, 1939)
Spread Spectrum (1940s)³

Some of them have become obsolete since then, but others are still with us and, as you see, they are very different, and use different technologies, media, methods … At the time, different technicians were taking care of them and nobody expected all these things to be unified under a general structure. Moreover, some communication systems were perceived as spooky and unsettling: hearing the voice of somebody at a distance, coming out of some small device, weird! The existence of such feelings can be traced in the literature of the time, for example in a short story by Dickens, “The Signal-Man”, where telegraph communication is related to ghosts’ appearances, or in a story by Kipling, “Wireless”, where some experiments with radio waves trigger a trance in one of the characters, put him in spiritual communication with Keats and make him rewrite a poem of his⁴. The fact that these technologies were associated with magic and paranormal activities by popular fiction writers hints at how they were still somewhat ‘mysterious’ in a deeper sense: hard to completely control, not yet domesticated by science.
Shannon was indeed the first to succeed in what Aspray calls “the scientific conceptualization of information⁵”, but somebody else had been already thinking about improving communication systems by identifying general descriptions and methods, most notably two engineers working at the Bell Labs, Harry Nyquist and Ralph Hartley. In two papers – Nyquist’s “Certain Factors Affecting Telegraph Speed” (1924) and Hartley’s “Transmission of Information” (1928) – they both still related to specific practical problems, and yet they were already elaborating on more abstract and universal concepts: Nyquist had a promising intuition about the “optimum code”, and his definition of “intelligence” anticipated Shannon’s information, while Hartley warned about the need of getting rid of “psychological considerations” in order to measure information with quantitative methods, and suggested to consider the message as a fully arbitrary selection out of all possible messages – semantics being irrelevant to the engineering problem. Shannon – who worked at the Bell Labs from 1941 to 1972 – credits the two papers from the 20s as basis for his work in the second sentence of his 1948 landmark paper: What is he adding to that, what are his main contributions? One is the mathematical modeling of information as a probabilistic system (already discussed in the previous chapter); the other is the examination of the message’s transmission through a (noisy or noiseless) channel, including the quantification of its physical limits and of the effects of noise. These are possibly the main parts of the theory: first the conceptualization, then the analysis. Shannon classified communication systems into three main categories: discrete (both signal and message are discrete, as in the telegraph), continuous (both signal and message are continuous, as in TV or radio), and mixed (including both discrete and continuous variables, as in the PCM speech transmission). Discrete noiseless systems are treated first, functioning as the “foundation” on which the other cases will build.

It is interesting to take a look at the ‘evolution’ of the equations proposed by the three scientists:

W = K log m (Nyquist)

where W is the speed of transmission of intelligence, m the number of values and K a constant;

H = log Sⁿ (Hartley)

where H is the amount of information, S the number of symbols and n the number of symbols in the transmissions;

H = – ∑ p_i log p_i (Shannon)

where H is the amount of information or entropy, and the ps are the probabilities of each given symbol (or “possible event”, as Shannon put it).
The recurring logarithmic function was an intuitively good and practical choice. A simple case provided by Shannon himself in the Prediction paper can help us understand how that works: if we consider the English twenty-six letter alphabet (i.e. excluding space and punctuation), and ignore completely the statistical properties of the letters, then the calculation of the entropy H according to Shannon’s law is reduced to

H = log₂ 26 = 4.7 bits per letter

The logarithm base 2, also called binary logarithm, corresponds to the binary digit as unit of measure. If we simplify even more and consider an alphabet composed by the four symbols A, B, C, D, each having 0.25 probability

H = log₂ 4 = 2 bits per letter, corresponding to two yes/no questions, or guesses, such as:

1. Is it either A or B? Yes.
2. Is it A? No.
Answer: It is B.

Or

1. Is it either A or B? No.
2. Is it C? No.
Answer: It is D.

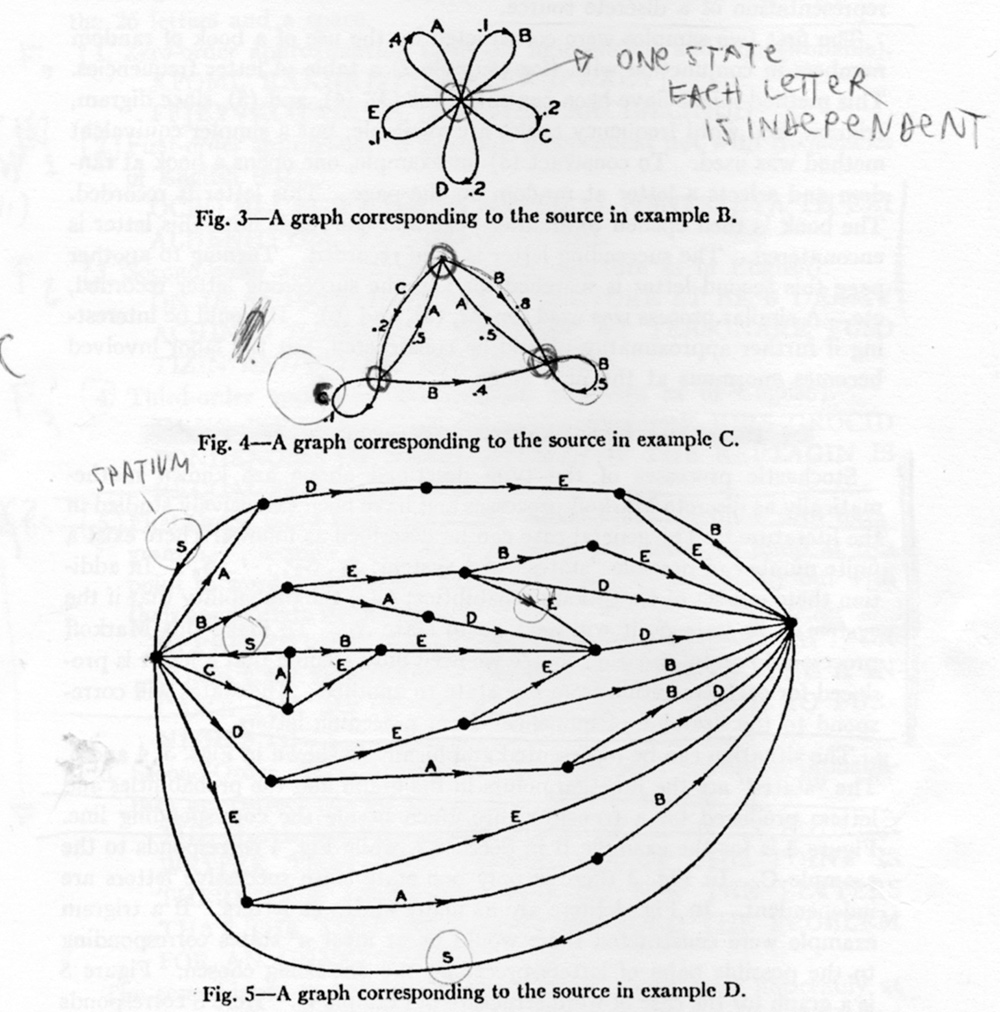
Graphic representation of Markov’s processes, from Shannon, “A Mathematical Theory of Communication”, 1948.

A discrete source that generates messages symbol by symbol, based on statistical properties – as was the case with the printed English language we examined – can be represented with graphs (see image above – they look beautiful!) You can imagine that, each time you guess/predict the next letter, you go through a transition (represented by a line) and reach a state (represented by a dot or node). The flower-like graph depicts a one-state system, in which you are free to choose any letter at any time, while the other two graphs are a bit more complex and present some constraints: depending on where you are, you can go only to certain states next. The Google Page Ranking algorithm is described by a graph of this kind where the states are webpages and the transitions are hyperlinks – yes, you can make big money with these things. And yet, ironically, the apparently unstoppable billionaire rollercoaster was somewhat triggered in the early 20th century by a Russian mathematician, Andrey Andreyevich Markov, who was a champion of pure mathematics, didn’t care at all about any application and didn’t want to dignify or justify mathematics with its usefulness – let alone its profitability. He discovered this special kind of probabilistic – or stochastic – processes where the variables have a statistical dependence from one another by analyzing literary texts from a quantitative point of view, namely the most popular book after the Bible in Russia at the time, Pushkin’s Eugene Onegin. Ergodic processes are a special class of Markov processes that possess statistical homogeneity and are represented by an aperiodic ‘closed-circuit’ graph. A graph that is not ergodic as a whole may contain ergodic subgraphs. Ergodic processes have a great significance in communication theory, because the coherence of their statistical properties will allow you to make good predictions once you have a big enough sample to work with.

You can study such processes by analyzing something that already exists, like a book, as Markov did, but you can also do it by generating something new, for example an artificial language that approaches English (or another language) in a gradually more complex way, starting with random letters (level 0), then taking into account the frequency of the single letters, of groups of two letters, three letters, words – just like the series of approximations F₀, F₁, F₂, … F_N, F_word of Shannon’s Prediction paper. The most complex samples start looking and sounding like regular English, not yet showing but hinting at the possibility of meaningful texts written by a machine. Artists, writers and scholars have shown interest in the ‘automation’ of human creativity for centuries already. An example in regards of the production of texts is the Engine, a fictional machine described in Jonathan Swift’s Gulliver’s Travels (1726), whose complex mechanical combinatory system operated with iron handles would allow even completely ignorant people to write meaningful texts about politics, physics, religion, whatever topic, “without the least assistance from genius or study.”

The aforementioned “Universalbibliothek” (universal library) by the German Kurd Laßwitz is a proto-science fiction short story published in 1904. A thought experiment is discussed in an upper middle-class drawing room: what if it were possible to create a library that included all books, meaning not only all books ever written but all possible books, all possible combinations of letters? Such a library would be complete, but also inaccessible on several grounds: spatially immense (although not infinite), it would contain its own complete and correct catalogue as well as many wrong and incomplete ones, alternative versions and mash-ups of all famous books, books that nobody ever wrote, and, of course, loads of pure nonsense. Trying to establish some parameters, as is good practice in all kind of experiments, helps get the computation done, yet doesn’t overcome the usability issues. Laßwitz chose a standard alphabet of 100 symbols, and set the length of each volume to one million characters. The very first volume could consist of blank spaces only (the one we talked about earlier in regards of compression of texts); the second would consist of blank spaces only but one a, and so on. Meaning would come up sometime later, by chance. You may have learned about a very similar concept for a universal library from two texts by Borges, the essay “The Total Library” (1939) and the short story “The Library of Babel” (1941) – both were inspired by Laßwitz.
The dialog between human creativity and machines can get more emotional and narrative: “Der Monolog der Terry Jo” is a 1968 radio drama by Max Bense and Ludwig Harig inspired by a true and tragic story. In 1961, a family from Wisconsin was brutally murdered by their own skipper while traveling on a sailing craft. Only the little daughter Terry Jo survived, and managed to escape on a float in the ocean; she was found in a state of shock in the middle of the ocean a few days later. The monolog consists of gradually more complex computer-generated text – following a process of approximation similar to the one described above – that sort of reproduces the slow recovering of the girl, her struggle to start making sense again and tell her own story.

Once it was discovered that communication systems and channels have a common structure, it didn’t take long until somebody tried to mix them; this had huge consequences in the technology industry, of course, but also created the basis for plenty of experimentation in the arts – the first thing that comes to my mind is the oscilloscope connected to a beamer, resulting in a black line on a white background that reacts to the live sound, used during live performances by the legendary Finnish duo Pan Sonic (ex Panasonic); another is the project electr•cute, a fully analogue audiovisual performance where Polish artist Kasia Justka sends video to audio and back with highly abstract and noisy results. The list could continue, possibly forever, you may have other examples in mind or you could find many by simply browsing the chronology of big festivals such as Transmediale, CTM and Ars Electronica – and even more if you start exploring smaller, more obscure past and current gatherings.

Benthic octopus and clam at 1461 meters water depth. California, Davidson Seamount. 2002. NOAA/Monterey Bay Aquarium Research Institute.

Claude

Claude E. Shannon was twenty when he got two bachelor’s degrees in mathematics and electrical engineering at the University of Michigan, in 1936. This double background and his ability to conceptualize technical problems made him the right person to nail down information theory. Engineering is much more than “applied science”.
Shannon’s typical approach reduces a problem to its essentials, then applies suitable mathematical tools to them. In the case of information theory, the problem was communication and the main tool was probability theory. In a somewhat similar fashion, he applied Boolean logic to switching circuits (what became an award-winning master thesis written in 1937 at MIT), and algebra to population genetics (the theme of his 1940 PhD and possibly his least successful project ever)⁵. His wartime work in the field of cryptography was more directly related to the upcoming information theory, and led to the classified publication “Communication Theory of Secrecy Systems” (1945), declassified and published in the customary Bell System Technical Journal a few years later.
Besides being a precocious and productive genius whose work changed forever the face of our world, Shannon was also a funny guy. He built all sorts of robots and devices, some to make experiments, some to play with, including a maze-solver electromagnetic mouse, a machine to solve the Rubik’s cube, a flame-throwing trumpet and the notorious Ultimate Machine, consisting of a box with a little retractable mechanical hand, whose only function is to turn itself off whenever you turn it on. Shannon loved juggling and gambling, two activities he could of course look at from an abstract mathematical point of view in order to explain or perform them better, and in the later part of his life he developed a (not only mathematical) interest in the stock market.

Information theory is an immense universe: the many hints at interdisciplinary developments it seems to offer, the charm and apparent universality of its main elements and keywords are somehow too good to be true – already in 1956, Shannon himself warned about the dangerous elements of its growing importance: “[…] information theory […] is certainly no panacea for the communication engineer or, a fortiori, for anyone else.⁷” By ‘anyone else’ he didn’t mean here that much laymen, but rather scientists from other fields trying to fix some information theory in their own research – a possibility he didn’t exclude and considered promising in several cases, but presented as arduous, tedious and necessarily based on a thorough understanding of the mathematical foundation. Shannon’s distinguished colleague J. R. Pierce wrote that “to talk about communication theory without communicating its real mathematical content would be like endlessly telling a man about a wonderful composer yet never letting him hear an example of the composer’s music.⁸” I’m afraid the present text is quite lacking according to Pierce’s standards, but it’s hopefully a good start that’ll make you want to try and listen to some music yourself – most of the publications in the selected bibliography section are available for free online.

Alice Cannava edits and publishes Occulto, curates cultural events in several “Freie Szene” Berlin venues, works as a designer/coder and studies history of science and technology at the TU Berlin.